5 - Tableaux à un indice
Domaines d’utilisation
On utilise souvent les tableaux à un seul indice pour :
-
Calculer les statistiques de base (moyenne, écart-type, plus grande et plus petite valeur, …);
-
Trier, rechercher un élément en particulier ;
-
Afficher les informations traitées (avant ou après le tri, satisfont aux conditions voulues, etc .).
Très souvent, on lit un fichier de données, on crée les tableaux qui contiennent les informations voulues. Comme la notion de fichier n’est plus abordée dans IFT 1810, on montrera :
-
La manière de déclarer, d’initialiser le contenu de tableaux
-
La manière de déclarer, de remplir le contenu de tableaux avec de
valeurs aléatoires (fabriquées par l’ordinateur)
- La manipulation de ces tableaux.
Déclaration
Façon directe
Écrire les déclarations directes de 3 tableaux qui contiennent les informations relatives à un groupe de 15 personnes :
age : tableau des entiers représentant les âges des 15 personnes;
taille et poids : deux tableaux de réels.
int age[15];
float taille[25], poids[70];age est un tableau de 15 entiers. age[0], age[1], ..., age[14] sont 15 éléments du tableau age. Chacun est une variable de type entier.
taille est un tableau de 25 réels. Ses éléments sont taille[0], taille[1], ..., taille[24]. Chacun est une variable de type réel. etc .
La façon de déclarer directement les tableaux est simple.
Façon prévue pour IFT 1810
Déclaration :
Déclarer deux tableaux age, taille et d’initialiser leur contenu avec les informations suivantes :
25, 17, 20, 40, 22, 54, 19 ans
1.72, 1.68, 1.85, 1.64, 1.57, 1.69, 1.73 mètreSolution (pour IFT 1810)
int age[] = { 25, 17, 20, 40, 22, 54, 19 } ;
float taille[] = { 1.72, 1.68, 1.85, 1.64, 1.57, 1.69, 1.73 } ;
int nbPers= sizeof(age) / sizeof(int) ;Schéma d’un tableau
On représente (imagine) un tableau comme une commode à plusieurs tiroirs dont chaque tiroir contient un seul objet de même type, comme par exemple, dans le cas de la déclaration d’un tableau age de 15 éléments de type entier
int age[] = { 25, 17, 20, 40, 22, 54, 19 } ;age[0] 25
age[1] 17
age[2] 20
age[3] 40
age[4] 22
age[5] 54
age[6] 19Manipulations d’un tableau
- On parcours les indices d’un tableau avec la boucle for. Notez que le premier indice est zéro :
for (i = 0; i < nbElement; i++)
...- Pour le cours IFT 1810 on manipule un tableau en utilisant des indices. Les autres méthodes de manipulation (avec pointeur) seront présentées dans le cours suivant : IFT 1166.
Manipulation :
Avec les deux tableaux de la page précédente, écrivez les instructions permettant
-
De compter le nombre de personnes ayant 25 ans ou plus ;
-
De calculer la taille maximale ;
-
De calculer la taille moyenne.
/* Fichier Tableaux1.C
Ce programme permet de déclarer et d'initialiser le contenu
du tableau des âges et des tailles de 7 personnes.
Il permet aussi
1. de compter le nombre de personnes ayant 25 ans ou plus ;
2. de calculer la taille maximale ;
3. de calculer la taille moyenne.
*/
#include <stdio.h>
int main()
{
const int BORNE = 25; /* 1 borne pour les âges */
int age[] = { 25, 17, 20, 40, 22, 54, 19 } ;
float taille[] = { 1.72, 1.68, 1.85, 1.64, 1.57, 1.69, 1.73 } ;
int nbPers = sizeof(age) / sizeof(int) ;
int nb25OuPlus = 0; /* nombre de personnes ayant 25 ans ou plus */
float tailleMax = 0.0, /* taille la plus grande */
somTaille = 0.0; /* total des tailles */
int i ; /* pour la boucle for */
printf("Au total, on a %d personnes a traiter\n", nbPers);
for (i = 0; i < nbPers ; i++)
{
if (age[i] >= BORNE )
nb25OuPlus++;
somTaille += taille[i];
if (taille[i] > tailleMax)
tailleMax = taille[i];
}
printf("\nLe nombre de personnes ayant %d ans ou plus : %d\n",
BORNE, nb25OuPlus);
printf("\nLa taille la plus grande : %6.2f metre\n", tailleMax);
printf("\nLa taille moyenne : %6.2f metre\n", somTaille / nbPers );
printf("\n\n");
printf("Appuyez sur la touche Entree pour quitter");
fflush(stdin);
getchar();
return 0;
}Exécution :
Au total, on a 7 personnes a traiter
Le nombre de personnes ayant 25 ans ou plus : 3
La taille la plus grande : 1.85 metre
La taille moyenne : 1.70 metre
Appuyez sur la touche Entree pour quitterLe tri d’un tableau :
Le but d’un tri est de mettre en ordre les valeurs des éléments d’un tableau. Dans le cours IFT 1810, on présente une seule méthode de tri : le tri par sélection. Deux autres méthodes plus rapides (le tri rapide “Quick Sort” et le tri par arbre binaire) seront présentées dans le deuxième cours de programmation IFT 1166, IFT 1170 ou IFT 1179.
Tri par sélection
Pour comprendre cette méthode, on observe un tableau T qui contient 5 entiers (nbElement vaut 5 ) :
T(0) T(1) T(2) T(3) T(4)
50 25 34 17 48Avant tri
L’indice i = 0
Quelle sera la valeur à placer à l’indice 0? C’est manifestement la valeur 17 située à l’indice 3 dans le tableau. Pour nous, c’est évident.
Mais comment procéder pour que l’ordinateur puisse trouver l’indice 3 qui est l’indice contenant la valeur minimale (indMin)?
On initialise cet indice à i :
indMin = i; /* qui vaut zéro */On compare t[indMin] avec t[1], t[2], ..., t[4]. Quand on découvre une valeur qui est encore petite, on ajuste la valeur de indMin :
Pour j allant de 1 à 4 Faire
Si t[j] < t[indMin] Alors indMin = j
j vaut 1: t[1] < t[0]? <==> 25 < 50? Oui ==> indMin = 1
j vaut 2: t[2] < t[1]? <==> 34 < 25? Non ==> on ne modifie pas indMin
j vaut 3: t[3] < t[1]? <==> 17 < 25? Oui ==> indMin = 3
j vaut 4: t[4] < t[3]? <==> 48 < 17? Non ==> on ne modifie pas indMinAprès avoir comparé avec les autres valeurs dans le tableau, on a 3 comme valeur dans indMin. Est-ce que 3 est le même indice que i qui vaut actuellement 0? Non. Donc, on a trouvé une plus petite valeur que celle qui est à la position 0 dans le tableau, on échange (permute) t[0] et t[3] :
T(0) T(1) T(2) T(3) T(4)
17 25 34 50 48L’indice i = 1 :
Quelle sera la valeur à placer à l’indice 1? C’est bien évidemment 25 et cette valeur est déjà à la bonne position dans le tableau, soit à l’indice 1.
Comment faire en sorte que l’ordinateur puisse trouver l’indice 1 qui est l’indice contenant la valeur minimale (indMin) à partir de i = 1?
On initialise cet indice à i :
indMin = i; /* qui vaut actuellement 1 */On compare t[indMin] avec t[2], t[3], ..., t[4]. Quand on découvre une valeur qui est encore petite, on ajuste la valeur de indMin :
Pour j allant de 2 à 4 Faire
Si t[j] < t[indMin] Alors indMin = j
j vaut 2: t[2] < t[1]? <==> 34 < 25? ==> Non
j vaut 3: t[3] < t[1]? <==> 50 < 25? ==> Non
j vaut 4: t[4] < t[1]? <==> 48 < 25? ==> NonAprès avoir comparé avec les autres éléments du tableau, indMin vaut 1. Est-il le même indice que i (qui vaut 1)? Oui. Donc, on n’a pas besoin de permuter.
On a :
T(0) T(1) T(2) T(3) T(4)
17 25 34 50 48A titre d’exercice, faire la même simulation pour i = 2 et i = 3
Après avoir fait la simulation avec i = 2 et i = 3, on a donc :
T(0) T(1) T(2) T(3) T(4)
17 25 34 48 50On n’a pas besoin de le faire pour i = 4. En effet, pour un tableau de 5 éléments, si les 4 premiers sont déjà en ordre, le cinquième (t[4] en langage C) sera nécessairement le plus grand.
Algorithme pour trier un tableau T :
/* Du premier à l’avant-dernier élément Faire : */
Pour i allant de 0 à Nb_Element - 2 Faire
Début
indMin <---- i
/* Comparer avec le reste pour ajuster indMin */
Pour j allant de i + 1 à nbElement - 1 Faire
Si t[j] < t[indMin] Alors
indMin <-----j
/* Permuter, si nécessaire, t[i] et t[indMin] */
Si indMin est différent de i Alors
Permuter t[i] et t[indMin]
FinPermutation du contenu de deux variables :
Soient deux variables de même type a et b (ici de type “int”); a vaut 15 et b vaut 5 :
int a = 15, b = 5;Permuter A et B signifie changer le contenu de ces deux variables de la façon suivante : a vaudra 5 et b vaudra 15 après une bonne permutation.
Analysons l’exécution des deux instructions suivantes :
a = b;
b = a;L’instruction “a = b;” signifie qu’on dépose la valeur de b dans a. A vaut donc maintenant 5.
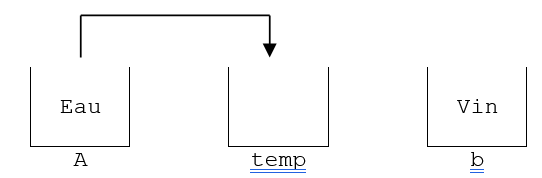
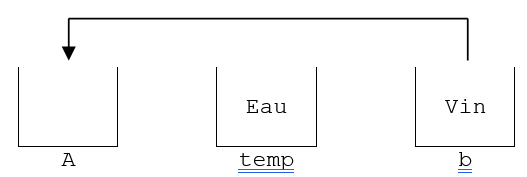
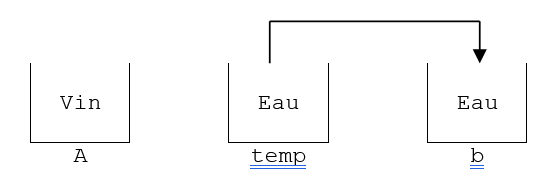
Puis, avec l’instruction “b = a;” on dépose a dans b, a devient donc la nouvelle valeur de b; b vaut donc maintenant 5. Ainsi, a vaut 5 et b vaut 5. Ceci n’est pas du tout une permutation. Pour permuter un verre de vin et un verre d’eau, on ne verse jamais l’eau dans le vin (b = a;). On utilise plutôt un troisième verre (un verre temporaire) :
À l’étape 1, on verse l’eau dans le verre temporaire (temp).
À l’étape 2, on verse le vin dans le verre d’eau.
À l’étape 3, on verse le verre temporaire dans le verre de vin.
Pour permuter a (vaut 15) et b (vaut 5) :
int a = 15, b = 5, temp;
temp = b;
b = a;
a = temp;On utilise ainsi une variable temporaire et trois affectations pour permuter le contenu de deux variables de même type.
Exemple 1 du tri par sélection
Écrivez un programme permettant de trier le tableau des âges :
int age[] = { 25, 17, 20, 40, 22, 54, 19 } ;
/* Fichier Tableaux2.C (exemple de tri par sélection)
Ce programme permet de déclarer et d'initialiser le contenu
du tableau des âges.
Il permet aussi de trier et d'afficher les âges, avant et après
le tri.
Voir Tableaux3.C pour le cas du tri quand on a plus d'un tableaux.
*/
#include <stdio.h>
int main()
{
int age[] = { 25, 17, 20, 40, 22, 54, 19 } ;
int nbPers = sizeof(age) / sizeof(int) ;
int i, j, indMin ; /* pour le tri et la boucle for */
int tempo; /* l'âge temporaire */
/* Affichage avant le tri : */
printf("Contenu avant le tri : ");
for (i = 0; i < nbPers ; i++)
printf("%4d", age[i]);
printf("\n");
/* Le tri par sélection : */
for (i = 0; i < nbPers - 1; i++){
indMin = i;
for (j = i + 1; j < nbPers; j++)
if (age[j] < age[indMin])
indMin = j;
if (indMin != i){
tempo = age[i];
age[i] = age[indMin];
age[indMin] = tempo;
}
}
/* Affichage après le tri : */
printf("\nContenu apres le tri : ");
for (i = 0; i < nbPers ; i++)
printf("%4d", age[i]);
printf("\n");
printf("\n\n");
printf("Appuyez sur la touche Entree pour quitter");
fflush(stdin);
getchar();
return 0;
}Exécution :
Contenu avant le tri : 25 17 20 40 22 54 19
Contenu apres le tri : 17 19 20 22 25 40 54
Appuyez sur la touche Entree pour quitterMise en garde : cas de plusieurs tableaux
Imaginez le cas simple suivant : on a deux tableaux : age et taille de 7 personnes (pages 107 et 108) :
int age[] = { 25, 17, 20, 40, 22, 54, 19 } ;
float taille[] = { 1.72, 1.68, 1.85, 1.64, 1.57, 1.69, 1.73 } ; i 0 1 2 3 4 5 6
age 25 17 20 40 22 54 19
taille 1.72 1.68 1.85 1.64 1.57 1.69 1.73Notez qu’avant le tri, la personne ayant 17 ans mesure 1.68 mètre.
Supposons qu’on veuille trier ces deux tableaux selon les âges. Si on ne fait rien
sur le tableau des tailles, on aura les informations suivantes :
i 0 1 2 3 4 5 6
age 17 19 20 22 25 40 54
taille 1.72 1.68 1.85 1.64 1.57 1.69 1.73=> après le tri, , la personne ayant 17 ans mesure 1.72 mètre !!!
On devient des chirurgiens au lieu d’être programmeurs!
Conclusion
Lors d’un échange pendant le tri, il faut échanger aussi les éléments correspondants dans les autres tableaux pour ne pas mélanger les informations. Voir l’exemple Tableaux3.C à la page suivante.
/* Fichier Tableaux3.C (exemple 2 de tri par sélection)
Ce programme permet de déclarer et d'initialiser le contenu
du tableau des âges et des tailles.
Il permet aussi de trier et d'afficher les deux tableaux, avant et
après le tri selon les âges.
*/
#include <stdio.h>
int main()
{
int age[] = { 25, 17, 20, 40, 22, 54, 19 } ;
float taille[] = { 1.72, 1.68, 1.85, 1.64, 1.57, 1.69, 1.73 } ;
int nbPers = sizeof(age) / sizeof(int) ;
int i, j, indMin ; /* pour le tri et la boucle for */
int tempoAge, /* l'âge temporaire */
tempoTaille; /* la taille temporaire */
/* Affichage avant le tri : */
printf("Contenu avant le tri :\n");
for (i = 0; i < nbPers ; i++)
printf("%2d) %6d %8.2f\n", i, age[i], taille[i]);
printf("\n");
/* Le tri par sélection : */
for (i = 0; i < nbPers - 1; i++){
indMin = i;
for (j = i + 1; j < nbPers; j++)
if (age[j] < age[indMin])
indMin = j;
if (indMin != i){
tempoAge = age[i];
age[i] = age[indMin];
age[indMin] = tempoAge;
tempoTaille = taille[i];
taille[i] = taille[indMin];
taille[indMin] = tempoTaille;
}
}
/* Affichage après le tri : */
printf("\n\nContenu apres le tri :\n");
for (i = 0; i < nbPers ; i++)
printf("%2d) %6d %8.2f\n", i, age[i], taille[i]);
printf("\n");
printf("\n\n");
return 0;
}Exécution :
Contenu avant le tri :
0) 25 1.72
1) 17 1.68
2) 20 1.85
3) 40 1.64
4) 22 1.57
5) 54 1.69
6) 19 1.73
Contenu apres le tri :
0) 17 1.68
1) 19 1.73
2) 20 1.85
3) 22 1.57
4) 25 1.00
5) 40 1.00
6) 54 1.00Voir l’exemple Tableaux4.C où on trie un gros tableau rempli avec des valeurs aléatoires.